Circles Part 2: Angle Relationships

Transformulas

Once similarity intuition has been built with circles, we can start getting into more specific relationships with angles and segments.  This post will look at using visual information from central angles and inscribed angles.

Pi Charts

http://wp.me/p464yb-2D

Students sometimes lack intuition for the measure of something.  Andrew Stadel has developed this idea into a thorough curriculum on estimation. In my classes we started reasoning through similar exercises.  Once we had a decent understanding of circle parts and whole, we moved on to other types of angles.

Non-Central Angles

At this point most students have the common sense that a circle has 360 degrees, and a triangle is half that at 180 degrees.  Built with this intuition in mind, we look at a triangle created by inscribed angles.

http://tube.geogebra.org/material/simple/id/115590

The next day we get to see the formula that collapses 3 ideas down to 1.

Dynamic Angles in…

View original post 372 more words

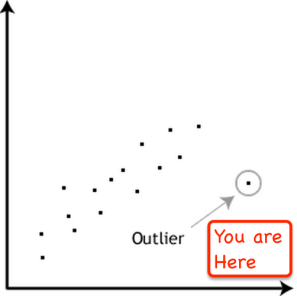
Outlier for Too Long #MTBoS30 8 of 30

This was me:

We are doing a unit on statistics in Integrated Math 1.  So far, I’m loving it (way more than I thought I would).

When I thought of basic statistics appropriate for High/Middle school, my mind wandered toward mean, median and mode.  I could work with these concepts decently enough.  I even understood how they were similar yet different.  Only now that statistics is a larger part of the CCSS curriculum am I taking it more seriously (better late than never).  We (myself and other integrating math 1 teachers in my district) are doing a unit that includes the basic descriptive statistics.  Now we’re working our way through linear regression and my appreciation for the content is increasing, in a concave up sort of way.  I’m see the big picture, or at least starting to.

First, we had covered the basics of descriptive statistics at the beginning of the school year.  We included some fun activities getting data from various things the students were involved with.  Recently we reviewed the content courtesy of some awesome practice via Khan Academy.  Yesterday and today the topic was correlation.  We focused on developing intuition and applying such insight toward predictions.  We used a great activity from @yummymath to try and make a prediction for how much the lifetime gross of Amazing Spiderman 2 will be.  We were able to also incorporate @desmos into the work to get some more pretty graphs.  Early next week our content team plans to continue with this topic going further and using some data from the students in the classroom.

The awesomeness today came from multiple students having the conversation about the strength of the correlation in a data set was only so-so because there were a few outliers that weren’t close to our guess for a line of best fit.  One student even used language like, “it’s not that strong cause it varies too much off the line.”  I didn’t prompt them to do it.  Nobody did.  They came up with half or more of the academic language without me defining it for them.  The students covered nearly all, if not all, of the CCSS SMPs with very little explicit direction on my part.

I feel slightly ashamed to not have had this appreciation for statistics before.  #facepalm  If you’re not including statistics and probability as a large part of your math curriculum, please ask yourself, “Why not?”  I consider myself a math geek and now I’m gaining a better overall understanding of how Stats ties in.  The support and opportunity it provides with math modeling and critiquing the arguments of others is invaluable.  I used to think that statistics was too “fuzzy” for me.  Not anymore.

New School Math, Old School Games #MTBoS30 4 of 30

This is Anthony (aka best bud):

We were playing this:

And we were talking about these:

Standards for Mathematical Practice

We focused on SMP 1 (making sense and persevering) as well as 7 (find /use structure).  Mostly 7.  Anthony and I are from the Sega and Nintendo  generation.  Beyond a tech ninja, volleyball all-star, and just an awesome guy, Anthony is a video game connoisseur in its truest form. There have been many a late night where we would stay up around the context of a video game, but it’s not just because we have to get that next achievement, or finish the level. Instead it’s the conversation.

I always enjoy our discussions that break down the elements of engagement and strategy of a game. As he and I were reminiscing on the design of a game as old as DuckTales, his wife Maira simply commented, “I don’t see it.” I immediately pictured the student in the classroom with the blank stare that says, “I don’t get it.” Learning is about structure. Those that can master the game identify and then manipulate this structure. We noted how a game often has predefined mechanics, and it is up to the user(s) to learn and then apply said mechanics. If you are in the world of education you should be seeing the correlation at this point. I’m not saying that video games = learning. What I am saying is the design structures built into gaming could teach us a lot about engagement and learning.  One could find plenty of discussion on this following the twitter feed #gblchat or #gamefication.

Anthony and I discussed how clever design of an interactive experience allows the user to identify relationships of objects, and then progressively learn more about such relationships in order to use them toward advancement. One of the games that is entirely dependent on this learning process is Portal.  A player has to identify how to use a simple set of tools in varied combinations to accomplish tasks.  Questions like,

• Does it matter the order in which I travel through these rooms?
• Is there another way I can use this tool?
• What will happen if I ______?
• Why is that platform there when clearly I can’t get to it right now?
• I can see an item through the window, but can’t reach it yet.  When will I come back to it?
• Why do I need to get that item?
• Can I use the items in combination such that an entirely new outcome is possible?

These are questions that a user intuitively asks and rarely articulates.  Such analyses happen so fast that most hardly bother to even out words to the thoughts.  The amateur simply play point and shoot while looking at the flashy colors and listening to the cool sounds.  In similar fashion the amateur student just comes with the simple tools and plays the game of school on Easy.  He/she might maintain low scores along the way but it doesn’t matter because you can often reset the level or maybe even purchase a power up for $.99.

The gamer/student progressing in his/her skill and performance takes advantage of the clues hidden within the game and exploits them.  The learning experience appears more like a puzzle worth solving, and the experience becomes self guided at times.  Those that excel in school aren’t better at memorizing formulas and passages.  The strong student is the one that can identify structure and use it.

For some teachers and learners though, this game of school is out of date, too simple to play, and tedious like no other.  We as educators need to take a bigger interest in the design of our game.  Not just the standards and outcomes, but the structure that guides the path of the user.  So where do we start?  I suggest following some tips from Dan Meyer.

Really, you should.  GO now and read it.